Neural Networks with Recurrent Generative Feedback
This blog takes about 10 minutes to read. It introduces the CNN-F model that introduces recurrent generative feedback to CNNs. The recurrent feedback reaches for a self-consistent prediction and improves adversarial robustness of its feedforward counterpart. Also check out the paper and code.
Introduction
Recent neuroscience findings suggest that recurrent feedback in the human brain is crucial for robust perception. Evidences show that adversarial examples can fool time-limited humans, and it takes longer for primates to perform core object recognition for challenging images than control images [1, 2].
Besides these empirical findings, computational neuroscience models aim to provide a principled explanation for recurrent feedback. According to the predictive coding theory, the feedback connections from a higher level of visual cortical area carry predictions of lower-level neural activities.
In this work, we extend the principle of predictive coding to explicitly incorporate Bayesian inference in neural networks via generative feedback connections. We define a form of self-consistency between the maximum a posteriori (MAP) estimation of the internal generative model and the external environment and enforce consistency in neural networks by incorporating recurrent generative feedback.
The proposed framework, termed Convolutional Neural Networks with Feedback (CNN-F), introduces generative feedback with latent variables into existing CNN architectures, making consistent predictions via alternating MAP inference. CNN-F shows considerably better adversarial robustness over regular feedforward CNNs on standard benchmarks.
Self-consistency
We propose the self-consistency formulation for robust perception. Intuitively, self-consistency says that given any two elements of {label, image and auxiliary information}, we should be able to infer the other one. Mathematically, we use a generative model to describe the joint distribution of labels, latent variables and input image features. If the MAP estimates of each one of them are consistent with the other two, we call a label, a set of latent variables and image features to be self-consistent.
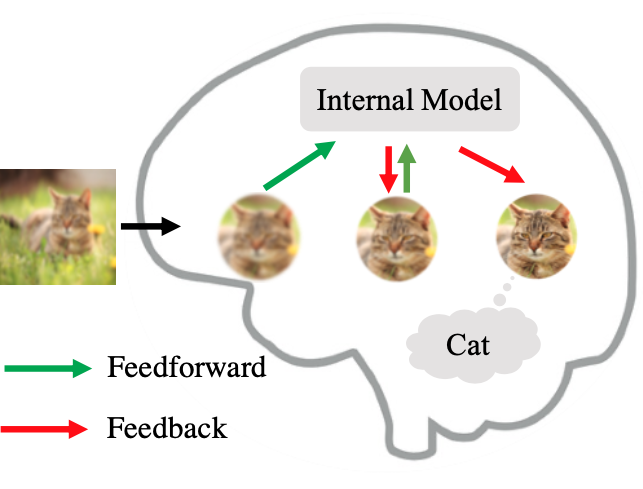
Consider the process of classifying a blurry cat. The blurry input is first processed by feedforward pathways. A label of “cat” is assigned by the internal model. After several cycles of feedforward and feedback, this leads to generation of a sharp image of a cat through the generative pathway. The reason is that the sharp image is the one that is maximally consistent with the input image and the internal generative model.
Generative Classifier
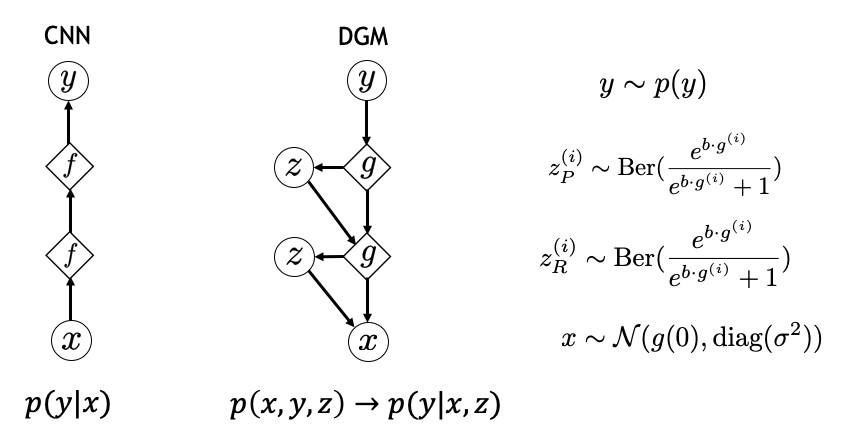
As we all know, to learn a classifier, we can directly learn the mapping from x to y, or p(y|x) from the input data. But there is also another way. That is, we learn the joint distribution of x and y, and compute p(y|x) using Bayes rule. p(y|x) computed this way is called a generative classifier. For example, logistic regression and Gaussian Naïve classifier is a discriminative and generative pair of classifiers that have the same parameterized form.

Since CNNs have achieved great success in image classification, we hope to have a generative model whose inference has the same architecture as CNN. It turns out that a recently proposed model called deconvolutional generative model (DGM) [3] satisfies this requirement.
In a DGM, an image is generated hierarchically from coarse to fine details. First, y is sampled from the label distribution. And features at the lower level, denoted by g here, is generated by deconvolutional operations.
For every entry g(i) in feature g, we also create a corresponding latent variable z(i). The latent variable is a switch, that is probabilistically set to 0 to 1 depending on the value of bg(i), where b is a bias parameter. Including this probabilistic switch is important because it allows the image generation process to be non-deterministic through its dependence on z.
The same generation process is repeated layer by layer. At the bottom level, we assume that image x has a Gaussian distribution centered at the generated image at the bottom layer.
Now we can compute the joint distribution p(x,y,z) by p(x|y,z)p(z|y)p(y). For a dataset with balanced label distribution, p(y) is a uniform distribution. Conditioning on y, we can compute the joint distribution of latent variables from the paramterized Bernoulli distributions. Finally, p(x|y,z) follows a Gaussian distribution centered at the generated image at the bottom layer g(0).
With the joint distribution, we can compute p(y|x,z) to get our generative classifier corresponding to CNNs.
Iterative inference and online updates in CNN-F
We need to compute the MAP inference of y, h, and z to enforce self-consistency. This is equivalent to find a local maximum of joint likelihood p(x,y,h) starting with an input x.
To achieve this, we iteratively fix two variables and find the optimal value for the third variable to increase the joint likelihood.
Starting from the input x, we encode x to feature space to get h. We feed h to the first forward pass that is the same as conventional CNNs. We set to be the prediction from the CNN and we set to be 1 if the value of the corresponding entry passes through ReLU.
Then we generate image feature from and to get , which is an updated version of input features. The newly generated image feature is fed back to the forward pass again for the next iteration.
We need to modify the ReLU and Pooling operators to AdaReLU and AdaPool to find that maximize the joint likelihood given h and y. Since depends on both h and y, AdaReLU and AdaPool take on not only the feedforward features but also the feedback features. AdaReLU passes through the value and set 1 to at the corresponding entry if the signs of feedforward features and feedback features match. AdaPool is defined in a similar way.
With AdaReLU and AdaPool defined, we prove that p(y|x,z) from the DGM has the same parametric form as a CNN with these modified nonlinear operators.
This iterative inference procedure is shown as follows. We repeat this process until it converges to a solution empirically.
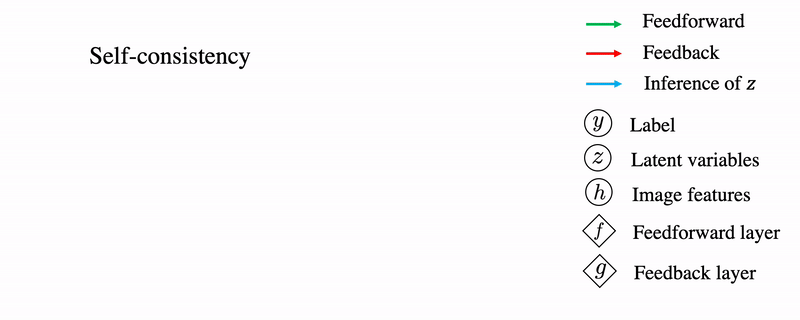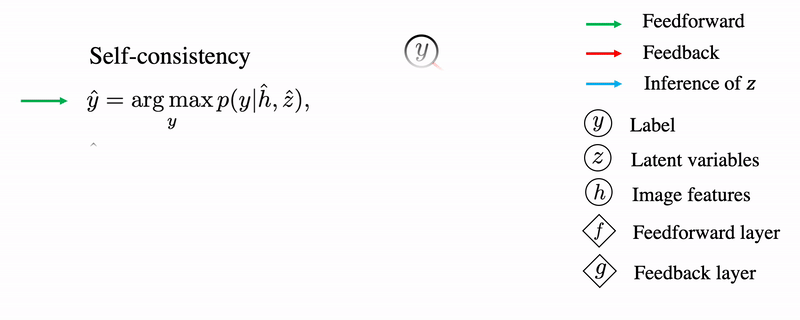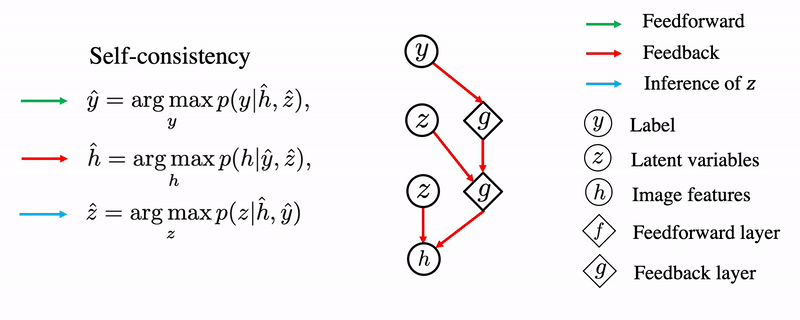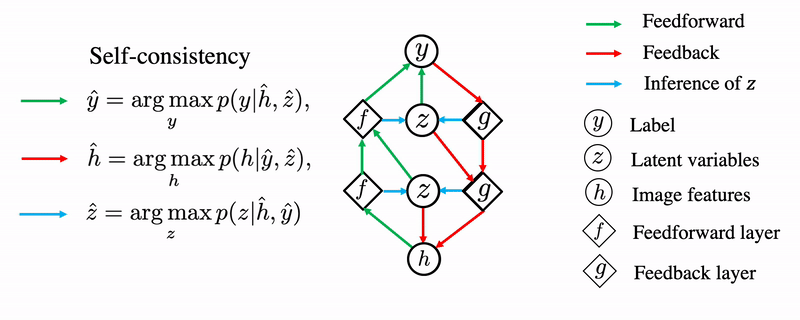
The forward and backward propagation in a CNN architecture is demonstrated here.
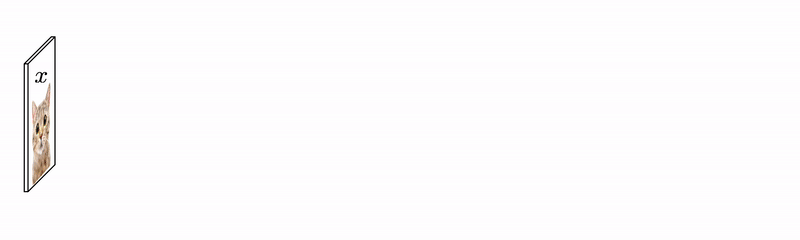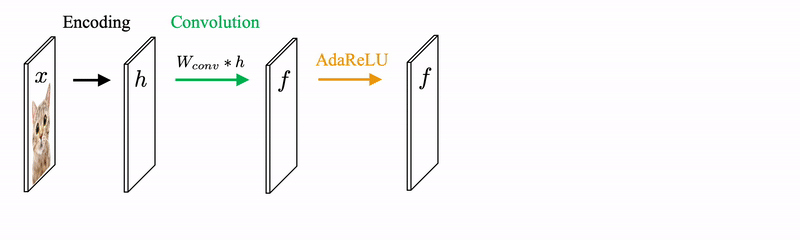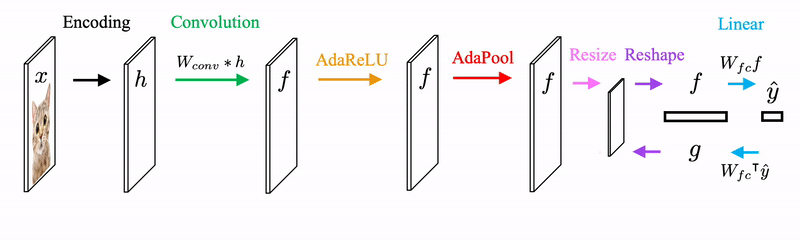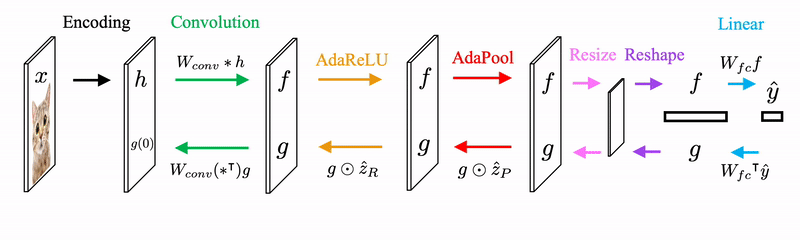
Results
Generative feedback promotes robustness
As a sanity check, we expect that CNN-F reconstructs the perturbed inputs to their clean version and makes self-consistent predictions. To this end, we verify the hypothesis by evaluating adversarial robustness of CNN-F and visualizing the restored images over iterations.
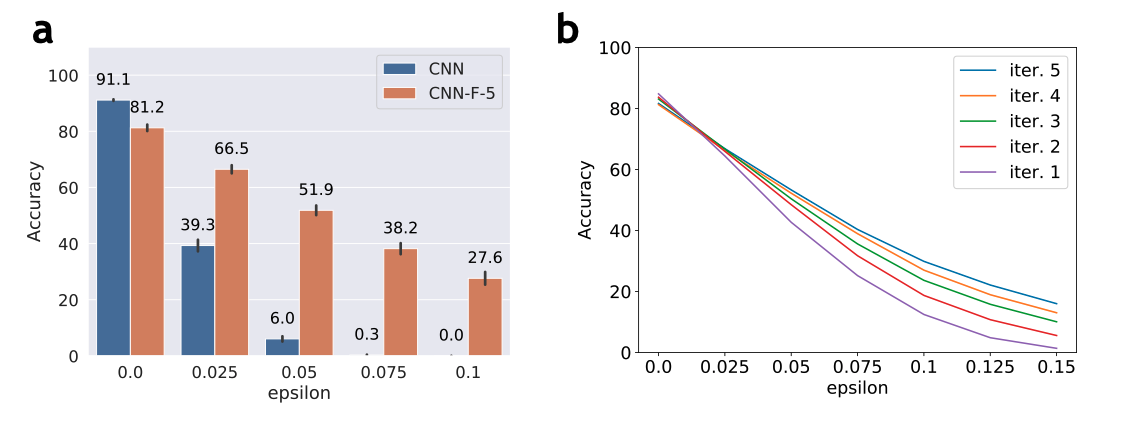
In the figure below, (a) shows that the CNN-F improves adversarial robustness of a CNN against Projected Gradient Descent (PGD-40) attack on Fashion-MNIST without access to adversarial images during training. (b) shows that the predictions are corrected over iterations during testing time for a CNN-F trained with 5 iterations. Furthermore, we see larger improvements for higher perturbation. This indicates that recurrent feedback is crucial for recognizing challenging images.
Furthermore, we find that CNN-F can repair distorted images over iterations. This means that the generative feedback is projecting distorted images to a clean domain where it is easier to reach self-consistent predictions.

Adversarial training
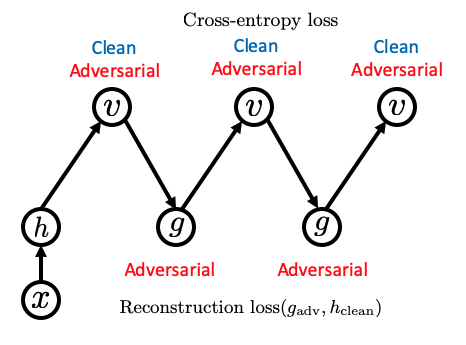
Adversarial training is a well established method to improve adversarial robustness of a neural network. We show that CNN-F can be combined with adversarial training to further improve the adversarial robustness. This figure illustrates the loss design we use for CNN-F adversarial training. stands for the perturbation maginitude of adversarial attack under L-inf norm.
In adversarial training, we want to provide a reference with clean feature for adversarial images to be denoised to over iteratoins. To guide the network achieving this goal, we use cross-entropy loss on both clean images and adversarial images and add reconstruction loss between generated features of adversarial samples from iterative feedback and the features of clean images in the first forward pass.
We train a CNN-F on CIFAR-10. We use Wide Resnet (WRN-40-2) as the architecture. To prevent gradient obfuscation when evaluating adversarial robustness, we use SPSA and transfer attack in addition to PGD-7 attack. We can also choose which iteration to attack in the CNN-F, first means attack the first iteration and e2e means end-to-end attack. The table below shows the adversarial accuracy of CNN-F with . We report two evaluation methods for CNN-F: taking the logits from the last iteration (last), or taking the average of logits from all the iterations (avg). We also report the lowest accuracy among all the attack methods with bold font to highlight the weak spot of each model.
| clean | PGD (first) | PGD (e2e) | SPSA (first) | SPSA (e2e) | Transfer | min | |
|---|---|---|---|---|---|---|---|
| CNN | 79.09 | 42.31 | 42.31 | 66.61 | 66.61 | —— | 42.31 |
| CNN-F (last) | 78.68 | 48.90 | 49.35 | 68.75 | 51.46 | 66.19 | 48.90 |
| CNN-F (avg) | 80.27 | 48.72 | 55.02 | 71.56 | 58.83 | 67.09 | 48.72 |
Conclusion
There are many evidences showing the existence of feedback connections in the brain. But the roles of these feedback connections remains a mystery. The possible answers might be generating lower level representations, directing attention, etc.
Inspired by the predictive coding theory, we propose a model with recurrent generative feedback. We perform approximate Bayesian inference to incorporate both feedforward and feedback signals in visual perception tasks. In the experiments, we demonstrate that the proposed feedback mechanism can considerably improve the adversarial robustness compared to conventional feedforward CNNs. Our study shows that the generative feedback in CNN-F presents a biologically inspired architectural design that encodes inductive biases to benefit network robustness.
References
- Gamaleldin F. Elsayed et al., Adversarial Examples that Fool both Computer Vision and Time-Limited Humans, NeurIPS, 2018
- Kohitij Kar et al., Evidence that recurrent circuits are critical to the ventral stream’s execution of core object recognition behavior, Nature Neuroscience, 2019
- Tan Nguyen, et al., A bayesian perspective of convolutional neural networks through a deconvolutional generative model. arXiv:1811.02657, 2018.